TOP
二分查找 旋转排序数组
整数数组 nums 按升序排列,数组中的值 互不相同 。
在传递给函数之前,nums 在预先未知的某个下标 k(0 <= k < nums.length)上进行了 旋转,使数组变为 [nums[k], nums[k+1], …, nums[n-1], nums[0], nums[1], …, nums[k-1]](下标 从 0 开始 计数)。例如, [0,1,2,4,5,6,7] 在下标 3 处经旋转后可能变为 [4,5,6,7,0,1,2] 。
给你 旋转后 的数组 nums 和一个整数 target ,如果 nums 中存在这个目标值 target ,则返回它的下标,否则返回 -1 。
来源:力扣(LeetCode) 链接:https://leetcode-cn.com/problems/search-in-rotated-sorted-array 著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
简单题解
// 解题前置信息如以下 TypeScript 伪代码
const findNumber = (number: number[], target: number): number => {};
let p = curIndex,
l = leftIndex,
r = rightIndex;
P = number[p]; // same as l L, r R这里,我们需要使用二分法找到中间节点,这里的中间节点的左右段中必然存在一段是有序片段,另一段必然是无序的,于是利用缩短区间的方法,可以将无序的片段逐步限制到有序来进行查找,有序查找使用常规二分方法即可。
⚡️ 所以简单总结成一句话就是:从中间切开,抛弃无效片段。
如有[4,5,6,7,8,1,2,3] target = 8:
- P = 7 故 [7,8,1,2,3],即抛弃了[4,5,6]。首先证明 7 的左边是递增的,接着有 7 < 8 ,所以左边可以直接抛弃。证明 7 的左边是递增的很容易,只需要 7 > 最左边的 4 即可(核心)
- P = 1 故 [7,8,1],抛弃了[2,3]。因为 1 的右边被证明是递增的,如果不是递增的,1 不可能 < 最右边的 3
- P = 8 ✅ 这是最理想的情况,否则重复上述过程直到找到可二分查找的片段。
详解
具体如何区分有效片段(包含 target 的那一段)见如下解答。
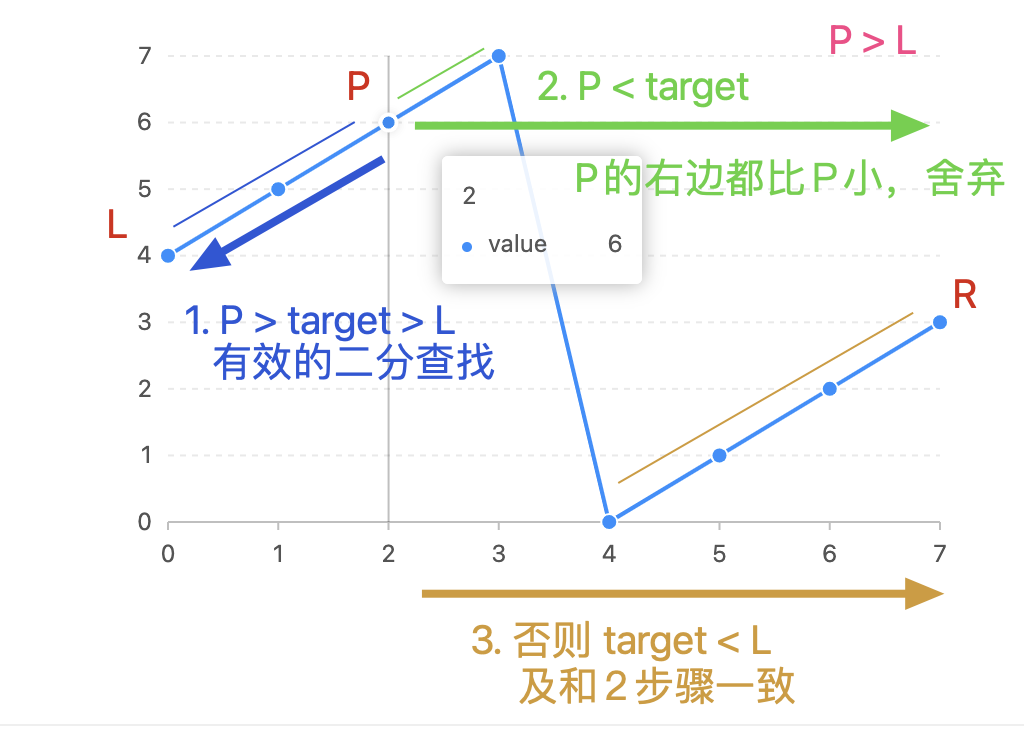
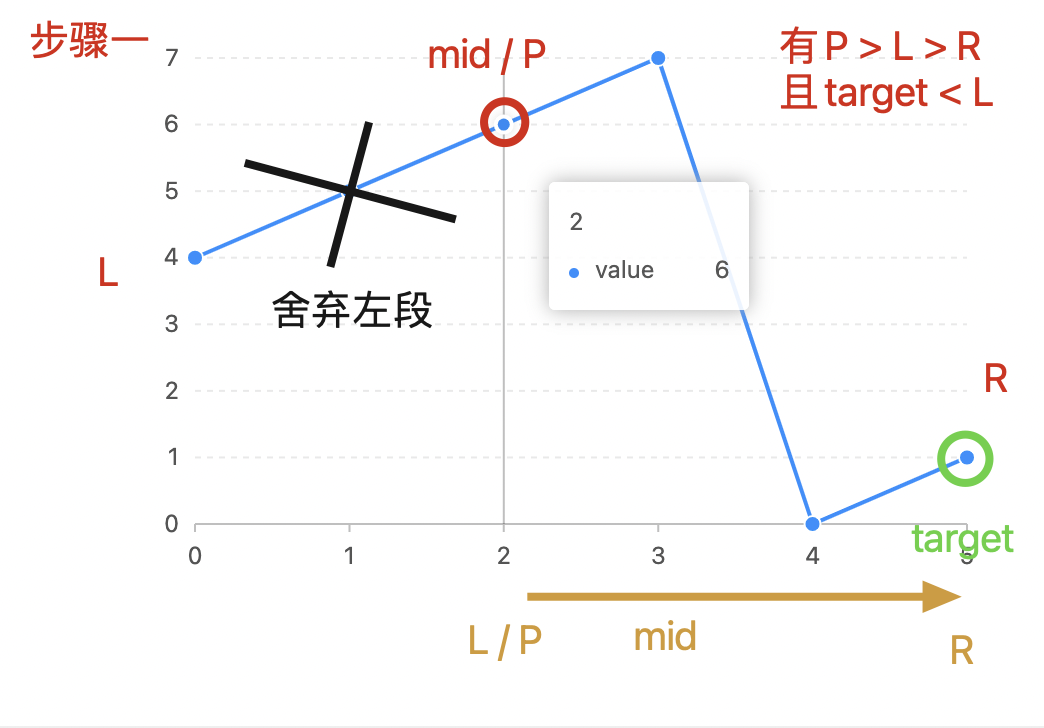
- 情况一:P > L > R
- 🟢 P < target, 舍弃
leftSlice-> 3. 我们要找的就是绿色的区间,不过这段区间在需要再进一步的进行限制,此时区间会限制在 [p, r] 之间 - 🔵 target > L, 已经确定区间,有效二分查找
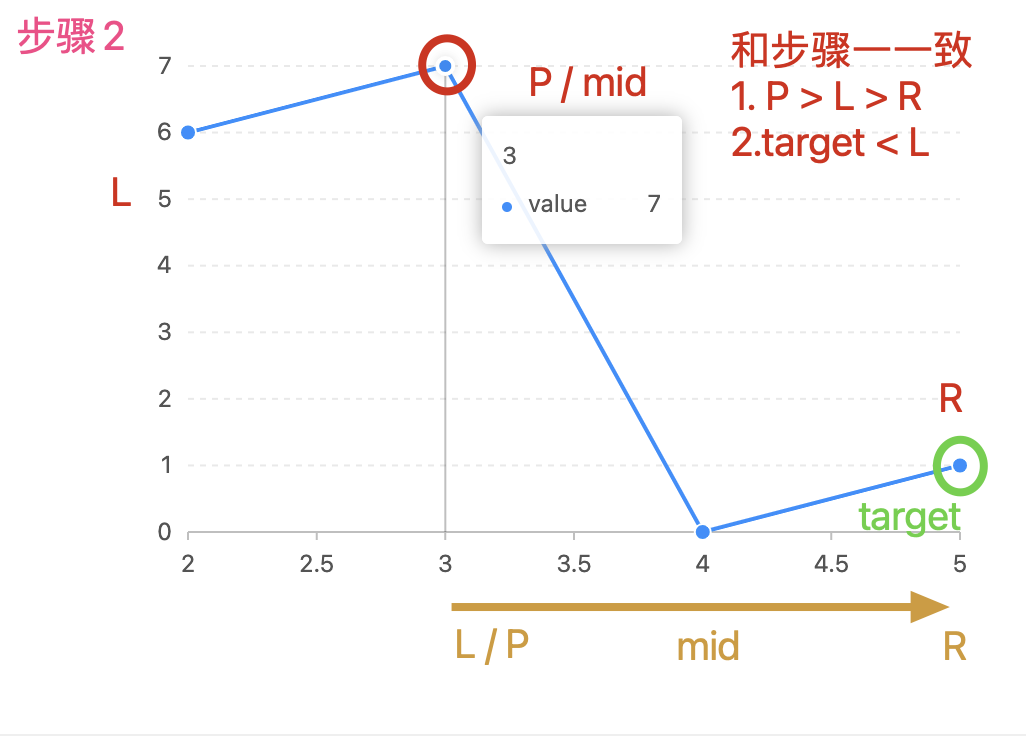
- 🟤 重复进行一次 P,L,R 的比较
- 🟢 P < target, 舍弃
-
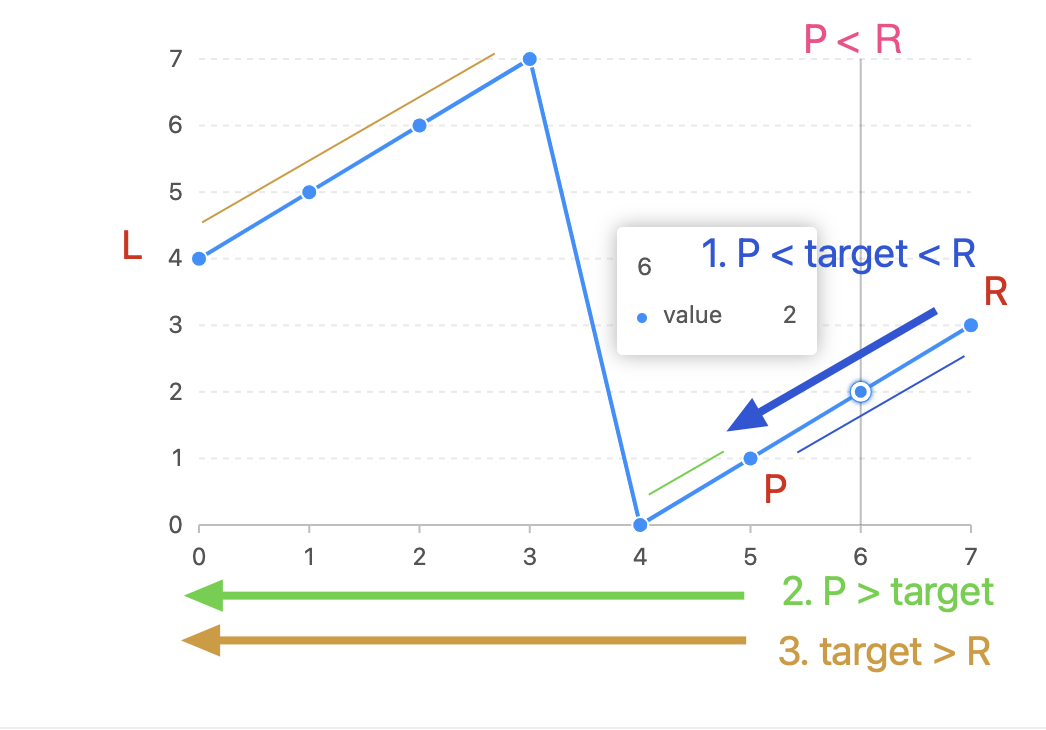
情况二:L > R > P
- 🟢 P > target, 舍弃
rightSlice-> 3. ,取左边不确定半段,再将左边半段重复以上过程直到可以运用二分查找 - 🔵 target < R, 确定区间,有效二分查找
- 🟤 重复进行一次 P,L,R 的比较
- 🟢 P > target, 舍弃
-
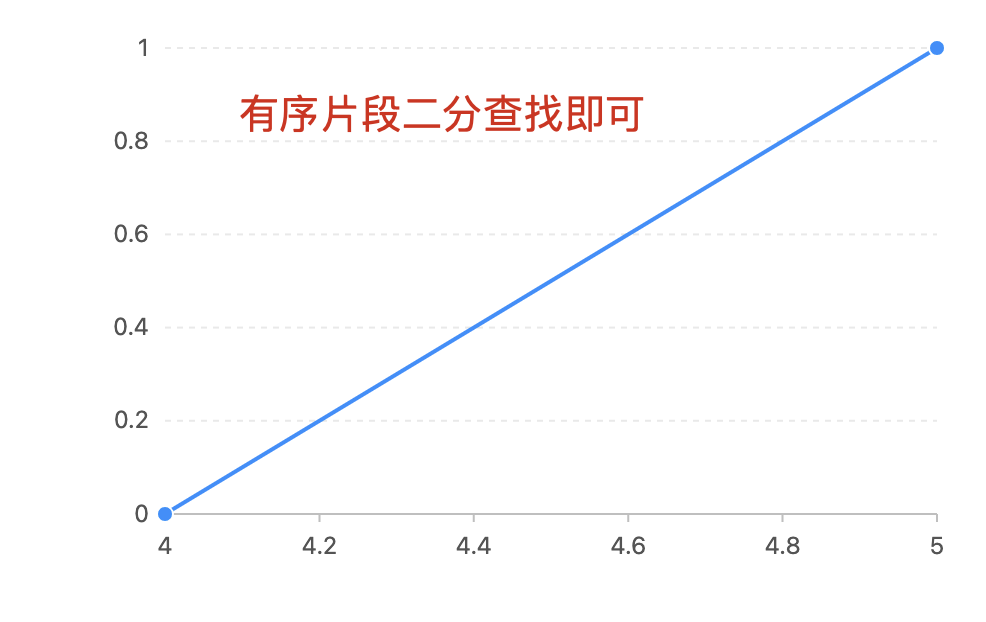
情况三: L < P < R ; 直接进行常规二分查找
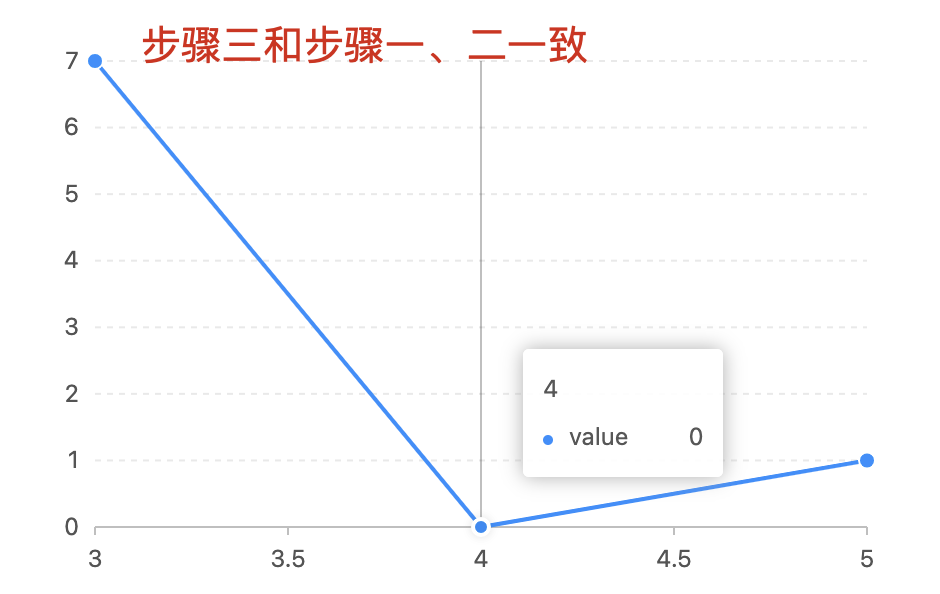
具体图例过程总结
举例有有[4,5,6,7,0,1] target = 1
相关代码
function search(nums: number[], target: number): number {
let left = 0,
right = nums.length - 1;
while (left <= right) {
// 防止溢出
const curIndex = Math.floor((left - right) / 2 + right);
if (nums[curIndex] === target) return curIndex;
if (nums[curIndex] > nums[left] && nums[curIndex] < nums[right]) {
// 有效二分
if (nums[curIndex] > target) right = curIndex - 1;
else left = curIndex + 1;
} else if (nums[curIndex] < nums[left]) {
// P < R
if (target <= nums[right] && target >= nums[curIndex]) left = curIndex;
else right = curIndex - 1;
} else {
// P > L
if (target >= nums[left] && target <= nums[curIndex]) right = curIndex;
else left = curIndex + 1;
}
}
return -1;
}